Martingale measure
The martingale property of an asset means that its current price is fair, that is, it reflects the discounted expected future payoffs. Martingale probability measures are often denoted by \(\mathbbm {Q}\) in the financial literature. We want to find martingale measures which are equivalent to the original probability measure \(\mathbbm {P}\). In our setting, equivalency holds if for the new probability measure all probabilities are strictly positive. The probability measure is hence \(\in \textrm{int}(\Delta ^K)\) and denoted by \(\varvec{q} \in \textrm{int}(\Delta ^K)\). The martingale property here reads as: \(\varvec{\Pi }= \mathbbm {E}_{\varvec{q}}[\varvec{S}].\) The corresponding probability measure \(\varvec{q}\) is called equivalent martingale measure or risk-neutral measure, whose existence is discussed below. Finding a risk-neutral measure is equivalent to finding the fair prices of the Arrow securities, which are also called state prices30. The state prices are in general not \(\ell _1\)-normalized, while the martingale measure is \(\ell _1\)-normalized. Under the risk-neutral measure, the expectation value of an Arrow security is the probability of the respective event,
$$\begin{aligned} \mathbbm {E}_{\varvec{q}}[A_{\omega }]= q_{\omega }. \end{aligned}$$
(2)
Putting together the martingale property, the expansion into Arrow securities of Eq. (1), and the property of the Arrow securities of Eq. (2) we obtain for the prices of the traded securities
$$\begin{aligned} \Pi _i= \mathbbm {E}_{\varvec{q}}[S_i] = \sum _\omega S_{i\omega } q_\omega . \end{aligned}$$
(3)
In matrix form this equation reads as \(\varvec{\Pi }= S\varvec{q}\). The set of solutions that are contained in the simplex is given by
$$\begin{aligned} {{\mathcal {Q}}}:= \{ \varvec{q} \in \textrm{int}(\Delta ^K): S \varvec{q} = \varvec{\Pi }\}. \end{aligned}$$
(4)
Depending on the problem this set is either empty, contains single or multiple elements, or an infinite number of elements. The existence of a solution is discussed below via a no-arbitrage argument. We note that linear programming formulations do not admit optimization over open sets, i.e., cannot work with strict inequality constraints. Thus, we work with the closed convex set
$$\begin{aligned} \overline{{\mathcal {Q}}}:= \{ \varvec{q} \in \Delta ^K: S \varvec{q} = \varvec{\Pi }\}. \end{aligned}$$
(5)
As all algorithms in this work are approximation algorithms, the sets \({\mathcal {Q}}\) and \(\overline{\mathcal {Q}}\) will be considered the same in practice.
Existence of martingale measure
Now we discuss the existence of a martingale measure, a property that is closely related to the non-existence of arbitrage in the market. Arbitrage is the existence of portfolios that allow for gains without the corresponding risk. A standard assumption in finance is that the market model under consideration is arbitrage-free.
Definition 6
(Arbitrage portfolios and no-arbitrage assumption) An arbitrage portfolio is defined as a portfolio with non-positive present value \(\varvec{v}^T \varvec{\Pi }\le 0\) and non-negative future value for all market outcomes \(S^T \varvec{v}\ge 0\), and at least one \(j\in [K]\) such that \((S^T\varvec{v})_j > 0\). The no-arbitrage assumption, denoted by (NA), states that in a market model such portfolios do not exist.
No arbitrage implies the existence of a non-negative solution \(\varvec{q}\ge 0\) via Farkas’ lemma.
Lemma 1
(Farkas’ lemma24) For a matrix \(S \in \mathbbm {R}^{(N+1)\times K}\) and a vector \(\varvec{\Pi }\in \mathbbm {R}^{N+1}\) exactly one of the two statements hold. Either there exists a \(\varvec{q} \in \mathbbm {R}^{K}\) such that \(S\varvec{q} = \varvec{\Pi }\) and \(\varvec{q} \ge \varvec{0}\), or there exists a \(\varvec{v} \in \mathbbm {R}^{N+1}\) such that \(\varvec{v}^T \varvec{\Pi }< 0\) and \(S^T \varvec{v} \ge \varvec{0}\).
The condition \(\varvec{q}\ge 0\) is sufficient in our case, given the discussion for Eq. (5). Farkas’ lemma can be extended to the case \(\varvec{q}>0\)42,43 (see for example,24, Example 2.20 & Exercise 2.23). Expressing Lemma 1 in words, in the first case the vector \(\varvec{\Pi }\) is spanned by a positive combination of the columns of S. In the second case, there exists a separating hyperplane defined by a normal vector \(\varvec{v}\) that separates \(\varvec{\Pi }\) from the convex cone spanned by the columns of S. This lemma is immediately applicable to the arbitrage discussion. By Definition 6, existence of arbitrage is
$$\begin{aligned} \exists \, \varvec{v} \in \mathbbm {R}^{N+1} \text { such that: } \varvec{v}^T \varvec{\Pi }\le 0, \, S^T \varvec{v} \ge \varvec{0} \text { and } \exists j\in [K] \text { such that } (S^T\varvec{v})_j > 0. \end{aligned}$$
(6)
It is easy to see that the following condition implies Eq. (6),
$$\begin{aligned} \exists \, \tilde{\varvec{v}} \in \mathbbm {R}^{N+1} \text { such that: } \tilde{\varvec{v}}^T \varvec{\Pi }< 0 \text { and } S^T \tilde{\varvec{v}} \ge \varvec{0}, \end{aligned}$$
(7)
since from \(\tilde{\varvec{v}}\), we can construct the \(\varvec{v}\) in Eq. (6) by adding the amount \(\vert \tilde{\varvec{v}}^T \varvec{\Pi }\vert\) to the first component2. Then, by negation, if \((\textbf{NA})\) holds, Farkas’ lemma implies that case (i) holds, as case (ii) is ruled out. Since there exists a \(\varvec{q} \ge 0\) such that \(S\varvec{q} = \varvec{\Pi }\), the set \(\overline{{\mathcal {Q}}}\) is by its definition not empty. In conclusion, assuming the absence of arbitrage implies that \(|\overline{{\mathcal {Q}}}| \not = 0\). Together with the reverse direction, one obtains the “first fundamental theorem of asset pricing”2.
Linear programming formulation of asset pricing
We reduce the problem of derivative pricing to two linear programs, corresponding to the finding of the maximum and the minimum price of the derivative. For pricing, we use any risk-neutral probability vector \(\varvec{q} \in {\mathcal {Q}}\), if the set is not empty (i.e., under the no-arbitrage assumption). Lacking any other information or criteria, any element in \({\mathcal {Q}}\) is a valid pricing measure. The derivative is priced by computing the expectation value of the future payoff under the risk-neutral measure \(\varvec{q}\), (discount factors are taken to be 1)
$$\begin{aligned} \Pi _{D,\varvec{q}} := \mathbbm {E}_{\varvec{q}}[{D}] = \sum _{\omega \in \Omega } D_\omega q_\omega . \end{aligned}$$
(8)
The price \(\Pi _{D,\varvec{q}}\) is in our setting an inner product between the pricing probability measure \(\varvec{q}\) and the vector describing the random variable of the financial derivative. Since \({\mathcal {Q}}\) is convex2, it follows that the set of possible prices of the derivative is a convex set, i.e., an interval. We can formulate as a convex optimization problem the problem of obtaining the maximum and minimum price \(\Pi _{{D},\min }\) and \(\Pi _{{D},\max }\), respectively, which are possible over all the martingale measures. We obtain two optimization programs:
$$\begin{aligned} \Pi _{{D},\max }:= & {} \max _{\varvec{q} \in {\mathcal {Q}}} \mathbbm {E}_{\varvec{q}}[{D}], \end{aligned}$$
(9)
$$\begin{aligned} \Pi _{{D},\min }:= & {} \min _{\varvec{q} \in {\mathcal {Q}}} \mathbbm {E}_{\varvec{q}}[{D}] . \end{aligned}$$
(10)
when the solution of the optimization problems is a large range of prices, additional constraints can be added to narrow the range of admissible prices. We discuss a simple case study in the main part (with further details in Methods), where for a highly incomplete market we can narrow the range of admissible prices of a derivative to its analytic price with a regularization technique. In general, additional non-redundant assets reduce the number of valid risk-neutral measures by making the market more complete, and thus reduce the range of admissible prices.
In the following, we discuss the maximizing program Eq. (9), as the minimizing program is treated equivalently. We make explicit the LP formulation of the problem in Eq. (9). The first step is to replace the open set \({\mathcal {Q}}\) with the closed set \(\overline{{\mathcal {Q}}}\). In that sense, we do not find probability measures that are strictly equivalent to \(\mathbbm {P}\). However, the probability measures in \(\overline{{\mathcal {Q}}}\) are arbitrarily close to the equivalent probability measures in \({{\mathcal {Q}}}\). We use vector notations and the price system to write the linear program
$$\begin{aligned} \max \limits _{\varvec{q} \in \mathbbm {R}^K} \varvec{D}^T \varvec{q} \quad \text {s.t.} \quad \varvec{q} \ge 0,\ S\varvec{q} = \varvec{\Pi }. \end{aligned}$$
(11)
From Supplementary Material, we see that the dual of the maximizing program is given by a linear program for the vector \(\xi \in \mathbbm {R}^{N+1}\) as
$$\begin{aligned} \min \limits _{\xi \in \mathbbm {R}^{N+1}} \varvec{\Pi }^T \varvec{\xi }\quad \text {s.t.} \quad \varvec{D} \le S^T \varvec{\xi }. \end{aligned}$$
(12)
The financial interpretation is the following. The dual program finds a portfolio of the traded assets \(\varvec{\xi }\) which minimizes today’s price \(\varvec{\Pi }^T \varvec{\xi }\). The portfolio attempts to replicate (or “hedge”) the derivative future payoff. Ideal replication would mean \(\varvec{D} = S^T \varvec{\xi }\), i.e, the payoff of the portfolio of assets is exactly the derivative outcome for all market outcomes. The linear program attempts to find a portfolio \(\xi\) that “superhedges” the derivative in the sense that \(\varvec{D} \le S^T \varvec{\xi }\).
In the Supplementary Material, we discuss in Lemma 4 how to cast the LP optimization problem in standard form, as per Definition A.5 in the Supplementary Material. To map the problem into a zero-sum game we require the parameters defining the LP to assume values in the interval \([-1, 1]\). For this, we need to assume knowledge of the following quantities.
Assumption 1
(Assumptions for conversion to standard form LP) Assume the following:
-
Knowledge of \(D_{\max }:= \max \limits _\omega D_\omega\), the maximum payoff of the derivative under any event.
-
Knowledge of \(S_{\max }:= \max \limits _{ij} S_{ij}\), the maximum entry of the payoff matrix S.
Quantum input model
We discuss the input model of our quantum algorithm and a way of obtaining quantum sampling access to probability distributions. We assume access to the price system and the derivative in the standard quantum query model44 as follows.
Definition 7
(Quantum access to price system and derivative) Consider a price system as in Definition 2 and a derivative as in Definition 3. We say that we have quantum access to the price system and derivative if we have access to unitaries that perform \(\vert jk\rangle \vert 0\rangle \rightarrow \vert jk\rangle \vert S_{jk}\rangle\), \(\vert j\rangle \vert 0\rangle \rightarrow \vert j\rangle \vert \Pi _{j}\rangle\), and \(\vert k\rangle \vert 0\rangle \rightarrow \vert k\rangle \vert D_{k}\rangle\) at unit cost, where \(j\in [N_1]\), \(k\in [N_2]\), and all numbers are encoded to fixed-point decimal precision.
In many practical cases such as conventional European options, the query access to the derivative \(\varvec{D}\) can be obtained from a quantum circuit computing the function used to compute the derivative and query access to the payoff matrix S. We also define quantum vector access as the ability to construct a unitary that provides access to quantum states proportional to any vector in a subspace.
Definition 8
(Quantum vector access) We say that we have quantum vector access to d-dimensional vectors if, for any \(\varvec{x} \in \mathbb {R}^d\) with \(\Vert \varvec{x}\Vert _0 = s\) and \(\Vert \varvec{x} \Vert _2 \le \beta\), we can construct a unitary in time \(O\left( s\ \textrm{poly} \log d \right)\) that performs the mapping
$$\begin{aligned} \vert 0\rangle \mapsto \frac{1}{\sqrt{\beta }}\sum _{i=1}^d x_i \vert i\rangle \vert 0\rangle + \vert G\rangle \vert 1\rangle , \end{aligned}$$
in \(O\left( \textrm{poly} \log d \right)\) time, where \(\vert G\rangle\) is an sub-normalized arbitrary quantum state.
Further discussion on the quantum input model can be found in the Supplementary Material.
Quantum zero-sum game
The quantum algorithm for zero-sum games uses amplitude amplification and quantum Gibbs sampling to achieve a speedup compared to the classical algorithm. At the end of this section, we discuss the run time of the classical algorithm for solving LP based on the reduction to a zero-sum game. The quantum computer is used to sample from certain probability distributions created at each iteration. We state here the main result from31. An \(\varepsilon\)-feasible solution to our LP problem means that we can find a solution such that the constraint is relaxed to \(A\varvec{q} \le \varvec{c} + \varvec{1} \varepsilon\).
Theorem 1
(Dense LP solver31, Theorem 13) Assume to have suitable quantum query access to a normalized LP in standard form as in Lemma 4, with r, R (defined in Lemma 5) known, along with quantum vector access as in Definition 8 to two vectors \(\varvec{x} \in \mathbb {R}^{N_1}, \varvec{y} \in \mathbb {R}^{N_2}\). For \(\varepsilon \in (0,1)\), there exists a quantum algorithm that finds an \(\varepsilon\)-optimal and \(\varepsilon\)-feasible \(\varvec{y}\) with probability \(1-\delta\) using \({\widetilde{O}}\left( (\sqrt{K}+\sqrt{N}) \left( \frac{R(r+1)}{\varepsilon } \right) ^3 \right)\) quantum queries to the oracles, and the same number of gates.
Theorem 1, can be directly adapted to the martingale pricing problem to obtain Algorithm 1 which we detail in the Supplementary Material. We formalized the embedding of a LP into a zero-sum game in Lemma D.1 in the Supplementary Material. The following statement follows from Theorem 1.
Theorem 2
(Quantum zero-sum games algorithm for martingale pricing) Let \((\varvec{\Pi }, S)\) be a price system with payoff matrix \(S \in \mathbb {R}^{(N+1) \times K}\) and price vector \(\varvec{\Pi }\in \mathbb {R}^{N+1}\), and let \(\varvec{D}\in \mathbb {R}^{K}\) be a derivative. Assume to have quantum access to the matrix S and the vectors \(\varvec{D}\) and \(\varvec{\Pi }\) through Oracle 7, and two vectors \(\varvec{x} \in \mathbb {R}^{N_1}\), and \(\varvec{y} \in \mathbb {R}^{N_2}\) through quantum vector access as in Definition 8. Under Assumption 1, for \(\varepsilon \in (0,1/2)\), Algorithm 1 in the Supplementary Material estimates \(\Pi _{D, \max }\) with absolute error \(\varepsilon\) and with high probability using
$$\begin{aligned} {\widetilde{O}}\left( (\sqrt{K}+\sqrt{N}) \left( \frac{(r+1)}{\varepsilon }D_{\max }\right) ^3 \right) \end{aligned}$$
quantum queries to the oracles, and the same number of gates. The algorithm also returns quantum access to an \(\varepsilon\)-feasible solution \(\widetilde{\varvec{q}}\) as in Definition 8.
Along with the price, this algorithm also returns a \(\varepsilon\)-feasible solution \(\widetilde{\varvec{q}}\). This solution could be used to price other derivatives \(\varvec{D}\). Note that the original algorithm of Theorem 1 results in an absolute error \(\varepsilon\) for \(\alpha\), for the normalized problem, which then results in an absolute error of \(\varepsilon D_{\textrm{max}}\) for the value of the derivative. Finding a relative error results from combining the algorithm described in Theorem 2 with standard techniques in randomized algorithms. We refer to45 for more details. The procedure involves executing the algorithm with different values for the absolute error, in an exponential search for a lower bound for the quantity \(\Pi _{D,\max }\). The expected runtime to obtain a relative error is
$$\begin{aligned} {\widetilde{O}}\left( (\sqrt{K}+\sqrt{N}) \left( \frac{(r+1)}{\varepsilon }\rho \right) ^3\log (\rho )\log (\log (\rho )) \right) , \end{aligned}$$
where \(\rho = \frac{D_{\max }}{\Pi _{D, \max }}\). Recently, a new quantum algorithm for solving zero-sum games has been proposed46. We discuss the implication of this algorithm in the Supplementary Material.
Classical zero-sum games algorithm and condition for quantum advantage
As the quantum algorithm, the classical algorithm requires a number of iterations \(T=O\left( \left( \frac{(r+1)}{\varepsilon } D_{\max } \right) ^2 \log (\frac{NK}{\delta }) \right)\) to achieve the same error \(\varepsilon\) for \(\Pi _D\). The cost of the computation for a single iteration is dominated by the construction of a sampling data structure for two probability vectors of size \(O\left( N \right)\) and \(O\left( K \right)\), respectively. Hence, the classical run time of the algorithm is \(O\left( T (N+K) \right) = O\left( \frac{(N+K)(r+1)^2 }{\varepsilon ^2}D_{\max }^2\log {\frac{NK}{\delta }} \right)\). Now we focus on a condition that allows for the quantum algorithm to be faster than the classical counterpart. The run time of the algorithms depends on the parameter r, which we can relate to the number of assets required to hedge a derivative.
Remark 1
Consider the context of Lemma A.6 in the Supplementary Material and its dual formulation. For any vector \(\varvec{\xi }\in \mathbbm {R}^{N+1}\), let \(r(\varvec{\xi })=\sum _{j=1}^{N+1} \xi _j\) and note that \(\sum _{j=1}^{N+1} \xi _j \le \Vert \varvec{\xi }\Vert _1\). In addition, if \(\vert \xi _j\vert \le 1\), we have \(\Vert \varvec{\xi }\Vert _1 \le \Vert \varvec{\xi }\Vert _0\). In our setting, where \(\varvec{\xi }^*\) is the optimal portfolio and \(\Vert \varvec{\xi }^*\Vert _0\) is the number of assets in the optimal portfolio, we hence can use \(r \le \Vert \varvec{\xi }^*\Vert _0\).
To obtain an advantage in the run time of the quantum algorithm we have to presuppose the following for \(\varvec{\xi }\).
Theorem 3
If the derivative requires \(\Vert \varvec{\xi }^*\Vert _0 \le \frac{\varepsilon (\sqrt{N+K})}{D_{\max }}\) asset allocations to be replicated, then Algorithm 1 performs fewer queries to the input oracles compared to the classical algorithm.
Proof
To find the upper bound for r which up to logarithmic factors still allows for a speedup, the value r needs to be such that \((\sqrt{N}+\sqrt{K})\left( \frac{(r+1)}{\varepsilon }D_{\max }\right) ^3 < \frac{(N+K) (r+1)^2 }{\varepsilon ^2}D_{\max }^2\). It is easy to see that \(r+1 \le \frac{\varepsilon (\sqrt{N+K})}{D_{\max }}\). By Remark 1, we have an advantage in query complexity if the number of assets in the optimal portfolio \(\Vert \varvec{\xi }^*\Vert _0\) is bounded by \(\frac{ \varepsilon \sqrt{N+K}}{D_{\max }}\). \(\square\)
Linear programming martingale pricing with the Black–Scholes–Merton model
The Black–Scholes–Merton (BSM) model obtains the price for certain financial derivatives by analytically evaluating an expectation value of the future payoff under a risk neutral measure \(\mathbbm {Q}\). We show a use case in the context of our linear programming formulation starting from a discretization of the standard BSM framework. In our example the payoff matrix can be efficiently computed, and hence access to a large QRAM may be avoided. We show how additional constraints in the LP regularize the model, so to narrow the range of admissible prices closer to the BSM price. The range of prices can be made comparable to the analytic value of the derivative. In the BSM model, we know an initial probability measure \({\mathbb {P}}\), which may not be a martigale measure. In the linear programming framework, it is hence more appropriate to consider a measure change from this initial probability measure.
Pricing with a measure change
An importation notion in pricing is the change of measure from the original measure to the martingale measure. The change of measure is described by the Radon-Nikodym derivative, which is denoted by the random variable \(X:=\frac{d\mathbbm {Q}}{d\mathbbm {P}}\). We extend the main part of the paper by formulating the problem of pricing a derivative when we are given an initial probability measure \(\mathbbm {P}\) via a vector \(\varvec{p} \in \Delta ^K>0\). We consider the measure change to a new probability measure \(\mathbbm {Q}\) via the vector \(\varvec{q} \in \Delta ^K\). The Radon-Nikodym derivative in this context is an \(\varvec{x} \in \mathbbm {R}^K_+\) for which \(x_\omega := \frac{q_\omega }{p_\omega }, \forall \omega \in \Omega\). The martingale property for the assets under \(\mathbbm {Q}\) and the pricing of a derivative are formulated as
$$\begin{aligned} \Pi _j = \mathbb {E}_{\mathbbm {Q}}[S_j]= & {} \mathbb {E}_{\mathbbm {P}}[X S_j] = \sum _{\omega \in \Omega } p_\omega x_\omega S_{j\omega }, \end{aligned}$$
(13)
$$\begin{aligned} \mathbb {E}_{\mathbbm {Q}}[D]= & {} \mathbb {E}_{\mathbbm {P}}[X D] = \sum _{\omega \in \Omega } p_\omega X_\omega D_\omega . \end{aligned}$$
(14)
Hence, using \(\circ\) for the Hadamard product (element-wise product) between vectors, \(\varvec{D}[\varvec{p}] := \varvec{p} \circ \varvec{D}\) and \((S[\varvec{p}])_{j} := \varvec{p}\circ S_{j}\), we obtain the linear program for the maximization problem of Eq. (9) of the Radon-Nikodym derivative
$$\begin{aligned} \max \limits _{\varvec{x} \in \mathbbm {R}^K} \varvec{D}[\varvec{p}]^T \varvec{x} \quad \text {s.t.} \quad \varvec{x} \ge 0,\ S[\varvec{p}]\varvec{x} = \varvec{\Pi }. \end{aligned}$$
(15)
The minimization problem is obtained similarly.
Discretized Black–Scholes–Merton model for a single time step
In the BSM model, the market is assumed to be driven by underlying stochastic processes (factors), which are multidimensional Brownian motions. Multi-factor models have a long history in economics and finance47. The dimension and other parameters of the model, like drift and volatility, can be estimated from past market data48,49,50. We perform our first drastic simplification and set the number of risky assets to be \(N=1\). This makes the market highly incomplete but provides the analogue to the simplest BSM case. For the randomness, while the Brownian motion stochastic process has a specific technical definition, in the single-period model a Brownian motion becomes a Gaussian random variable. Hence, we assume here that we have a single Gaussian variable driving the stock. Under the measure \(\mathbbm {P}\), let B be a Gaussian random variable, also denoted by \(B\sim {\mathcal {N}}(0,1)\). The future stock price \(S_2\) is modeled as a function of B. In BSM-type models, asset prices are given by a log-normal dependency under \(\mathbbm {P}\),
$$\begin{aligned} S_2 = \Pi \ e^{\sigma B + \mu -\frac{1}{2}\sigma ^2}, \end{aligned}$$
(16)
using today’s price \(\Pi \in \mathbbm {R}_+\), the volatility \(\sigma \in \mathbbm {R}_+\), and the drift \(\mu \in \mathbbm {R}_+\). The stock price is not a martingale under \(\mathbbm {P}\), which can be checked by evaluating \(\mathbbm {E}_{\mathbbm {P}}[S_2] = \Pi e^\mu \ne \Pi\). However, it can be shown that under a change of probability measure, the Gaussian random variable can be shifted such that the resulting stock price is a martingale. The following lemma is a simple version of Girsanov’s theorem for measure changes for Gaussian random variables.
Lemma 2
(Measure change for Gaussian random variables51) Let \(B \sim {\mathcal {N}}(0,1)\) under a probability measure \(\mathbbm {P}\). For \(\theta \in \mathbbm {R}\) define \(B’:= B + \theta\). Then, \(B’ \sim {\mathcal {N}}(0,1)\) under a probability measure \(\mathbbm {Q}\), where this measure is defined by \(\frac{d \mathbbm {Q}}{d \mathbbm {P}} = \exp \left( -\theta B – \frac{1}{2} \theta ^2\right)\).
In standard Black–Scholes theory, we use \(\theta = \mu /\sigma\) to obtain \(B’ \sim {\mathcal {N}}(0,1)\) under \(\mathbbm {Q}\) where \(\frac{d \mathbbm {Q}}{d \mathbbm {P}} = \exp \left( -\frac{\mu }{\sigma } B – \frac{1}{2} \left( \frac{\mu }{\sigma }\right) ^2\right)\). Note that \(S_2\) satisfies the key property of a martingale as \(\mathbbm {E}_{\mathbbm {Q}}[S_2] = \mathbbm {E}_{\mathbbm {P}}\left[ \frac{d \mathbbm {Q}}{d\mathbbm {P}} S_2\right] = \Pi \ \mathbbm {E}_{\mathbbm {P}}[e^{\beta B -\frac{1}{2} \beta ^2}] = \Pi\), with \(\beta := \sigma – \mu /\sigma\).
We use the analytically solvable BSM model as a benchmark for the linear programming formulation. In order to fit this model into our framework, we discretize the sample space. We take a truncated and discretized normal random variable centered at 0 on the interval \([-6, 6]\). We take the sample space to be \(\Omega := \{-K_0,\cdots ,0,\cdots , K_0\}\) and \(K_0 \in \mathbbm {Z}_+\). The size of the space is \(K = \vert \Omega \vert = 2K_0+1\). The probability measure for \(\omega \in \Omega\), is \(p_\omega = e^{-\frac{36\omega ^2}{2 K_0^2}}/ \Sigma\), where \(\Sigma = \sum _{\omega \in \Omega } e^{-\frac{36\omega ^2}{2 K_0^2}}\). In analogy to the BSM model, we define the payoff matrix of future stock prices as
$$\begin{aligned} S_{1\omega }:= & {} 1, \nonumber \\ S_{2\omega }:= & {} \Pi \ e^{ {\sigma } B(\omega ) + \mu – \frac{1}{2}\sigma ^2}, \end{aligned}$$
(17)
where \(B(\omega ) = \frac{6\omega }{K_0}\). An important property of this example is that each \(S_{2\omega }\), can be computed in \(O\left( \log K \right)\) time and space via Eq. (17). For settings with more than a single asset \(N>1\), if we have more than one Gaussian random variables driving the assets, \(d>1\), we expect this cost to be \(O\left( d\log (NK) \right)\).
Regularization
Our optimization framework allows for a much larger set of Radon–Nikodym derivatives (all entry-wise positive K-dimensional vectors) than the set implied from the log-normal BSM framework. We observe that this freedom allows for a large range of prices corresponding to idiosyncratic solutions for the measure change. One method to overcome this issue is to include a larger number of non-redundant risky assets into the model. The assets make the market less incomplete and generally narrow the range of prices. As this strategy will also increase the complexity of the model, we pursue an alternative regularization strategy here.
To find solutions closer to the Black–Scholes measure change, we develop a regularization technique. This regularization is performed by including a constraint for the slope of \(\varvec{x}\) into the LP. The regularization leads to a narrowing of the range of admissible prices. The linear program in Eq. (15) optimizes over the set of measure changes
$$\begin{aligned} {\mathcal {M}}:= \left\{ \varvec{x} \in \mathbbm {R}^K \right\} , \end{aligned}$$
(18)
with the additional constraints given by the linear program. On the other hand, the Black–Scholes formalism essentially uses a particular measure from the one-parameter set of Gaussian measure changes (see Lemma 2)
$$\begin{aligned} {\mathcal {M}}_{\textrm{BS}}:= \left\{ \varvec{x}(\theta ) \in \mathbbm {R}^K\ \big |\ x_\omega (\theta ) = \exp \left( -\theta B(\omega ) – \frac{1}{2} \theta ^2\right) , \theta \in \mathbbm {R}, \omega \in \Omega \right\} . \end{aligned}$$
(19)
Optimizing over \({\mathcal {M}}\) finds a much larger range of prices, as the set \({\mathcal {M}}_{\textrm{BS}}\) is of course much smaller than \({\mathcal {M}}\). Via a regularization technique, we can find measures that are closer to the set \({\mathcal {M}}_{\textrm{BS}}\). Specifically, we add a first derivative constraint. Viewing \(\omega\) continuously, for the Girsanov measure change it holds that
$$\begin{aligned} \frac{\partial x_{\omega }}{\partial \omega } = \frac{\partial x_{\omega }}{\partial B} \frac{\text {d}B}{\text {d}\omega } = -\theta x_\omega \Delta , \end{aligned}$$
(20)
where \(\Delta := 6/K_0\). Since \(\omega\) is discrete, we obtain \(x_{\omega +1} – x_{\omega } \approx -\theta _0 x_{\omega } \Delta\) using \(\theta _0:= \mu /\sigma\). Employing this relationship as a constraint and using \(1/\eta >0\) as a closeness parameter, we optimize over the set
$$\begin{aligned} {\mathcal {M}}_{\textrm{reg}}(\eta ):= \left\{ \varvec{x}(\theta ) \in \mathbbm {R}^K\ \big |\ \left| (1 – \theta _0 \Delta ) x_\omega – x_{\omega +1}\right| \le \frac{1}{\eta }, \forall \omega \in \Omega \setminus \{K_0\} \right\} . \end{aligned}$$
(21)
Instead of using this particular regularization, there could be other approaches to narrow the range between admissible prices. As mentioned, an approach founded in theory2 is to complete the market with assets for which we know the price analytically/from the market. When there are more benchmark assets, we expect the range of prices to narrow, and in the limit of a complete market, every derivative has a unique price. We leave this approach for future work.
Call option
We define the common case of an European call option. The European call option on the risky asset gives the holder the right but not the obligation to buy the asset for a predefined price, the strike price. Hence, the future payoff is defined as \(D:= \max \left\{ 0, S_2 – Z \right\} ,\) where \(Z \in \mathbbm {R}_+\) is the strike price. Using the stock prices from Eq. (17), for a specific event \(\omega \in \Omega\) the payoff under \(\mathbbm {P}\) is
$$\begin{aligned} D(\omega ) = \max \left\{ 0, \Pi _i e^{ \sigma B(\omega ) + \mu -\frac{1}{2}\sigma ^2} – Z \right\} . \end{aligned}$$
(22)
Numerical tests
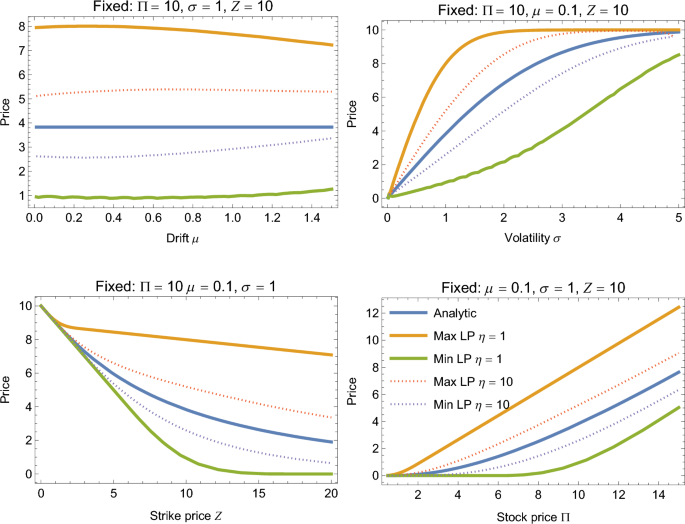
We test this approach for the call option, using the linear program in Eq. (15), its minimization form, and the payoff matrix Eq. (17). We compare the approach to the analytical price derived from the Black–Scholes–Merton model. We find that for a broad enough range of parameters, the analytic price of the derivative is contained in the interval of admissible prices given by the maximization and minimization linear programs of Eq. (15). The regularization is successful in recovering the BSM price for strong regularization parameter. In that sense, this linear programming framework contains the BSM model and allows modeling effects beyond the BSM model.
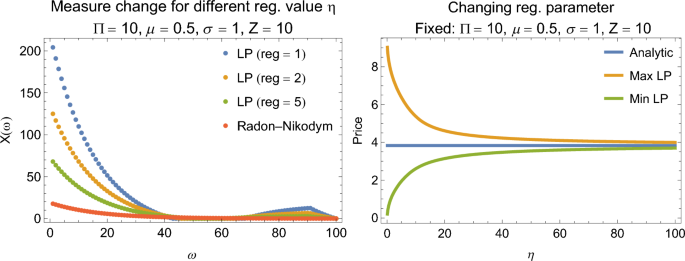
In the experiments as assume a payoff matrix of size \(S\in \mathbb {R}^{2 \times 100}\), i.e. \(N=1\) and \(K=100\), with the first row representing risk-less asset with payoff 1 in all the events. In our plots, we start with fixing the parameters \(\Pi =10\), drift \(\mu =0.5\) (and \(\mu =0.1\) for Fig. 1), volatility \(\sigma =1\) and strike price for the derivative of \(Z=10\). In most of the plots, the analytic value of the derivative is always within the range of the admissible prices of the minimization and maximization problem. The analytical dependencies are the standard BSM results48. Changing the drift does not influence the analytical price of the derivative, because the change of measure makes the price of the call option independent of \(\mu\). For benchmarking, in Fig. 2 we test different value for the regularization parameter. In picture (a) we find that the regularization parameter in the range of \(\eta \in \{1, 2, 5\}\) allows to get close to the analytic solution of the Radon-Nikodym derivative. In panel (b) we scan the value of the regularization parameter for \(\eta \in [0.1, 100]\). We observe that in our example, the solutions from the two LPs get closer to the analytic price as \(\eta\) goes larger.
Changing the regularization parameter. (Left panel) The Radon–Nikodym derivative obtained analytically is compared to the solution vector obtained from solving the linear program. (Right panel) The regularization parameter constrains the solution space and hence limits the admissible prices of the derivative.
Towards a quantum implementation
The requirement for an efficient quantum algorithm is to have quantum query access for the vectors (as in Definition 7) . For the payoff matrix S we can build efficient quantum circuits, without requiring large input data. To create the mapping \(\vert i,j\rangle \mapsto \vert i,j,S_{ij}\rangle\), we require classical access to input quantities such as drift and volatility, quantum access to the prices, and apply the arithmetic operations in Eq. (17). Following the same reasoning, since the vector \(\varvec{D}\) is efficiently computable from the matrix S, we can build efficient query access to its entries. We remark that such efficient computation can also hold for more complicated models, i.e., models that are more complicated than log-normal such as Poisson jump processes or Levy heavy-tailed distributions.
Quantum risk-neutral pricing in least-squares markets
With quantum linear systems algorithms, we can prepare a quantum state that is proportional to \(S^+ {\varvec{\Pi }}\), where \((\varvec{\Pi }, S)\) is a price system and \(S^+\) is the pseudo-inverse of the matrix S. The pseudo-inverse of S finds the minimum \(\ell _2\) norm solution to a linear system of equations; see also Theorem A.2 in the Supplementary Material. Unfortunately, this solution can lie outside the positive cone, and thus outside \(\textrm{int} (\Delta ^K)\), so we need a stronger no-arbitrage condition to guarantee to find a valid probability measure. Existence of an element in \({\mathcal {Q}}\) follows from the no-arbitrage assumption as discussed after Definition 6. We have to assume that one of the probability measures in \({\mathcal {Q}}\) is indeed also the minimum \(\ell _2\)-norm solution. A market satisfying this condition is what we call a least-square market. We note that the literature on incomplete markets has considered the pseudo-inverse of the payoff matrix before30. In general, positive solutions are obtained by adding suitable vectors from the nullspace to the pseudo-inverse solution52.
Definition 9
(Least-squares market) An arbitrage-free market model is called a least-squares market if \(S^+\varvec{\Pi }\in \mathcal {Q}\).
Under this assumption, the pseudo-inverse is guaranteed to find a positive solution to \(S \varvec{q}= \varvec{\Pi }\). This assumption is obviously stronger than the no-arbitrage assumption, which only implies that \(|\mathcal {Q}|\ne 0\). However, it is not as strong as assuming market completeness, which means that every possible payoff is replicable with a portfolio of assets. From the second fundamental theorem of asset pricing (see Theorem A.3 in the Supplementary Material), there exists a unique martingale measure if and only if every financial derivative is redundant, i.e., replicable via a unique portfolio of traded assets. If the market is not complete, a derivative is in general not replicated. The next theorem states that market completeness is a stronger assumption than the assumption of a least-square market.
Theorem 4
Let \((\varvec{\Pi }, S)\) be a price system. If the market model \(S \in \mathbb {R}^{(N+1) \times K}\) is complete, it is also a least-squares market.
Proof
Market completeness, via Theorem A.3 in the Supplementary Material, implies that \(|\mathcal {Q}|=1\), so there exists a unique measure \(\textbf{q}^*\in \mathcal {Q}\) such that \(\varvec{q}^*\in \textrm{int}(\Delta ^K)\) and \(S \varvec{q}^*= \varvec{\Pi }\). Furthermore, market completeness (via Lemma A.4 in the Supplementary Material), implies that the matrix S is square and has full rank. Define the pseudo-inverse solution as \(\varvec{q}^+:= S^{+} \varvec{\Pi }\). Since \(N+1=K\), and the assets are non-redundant, \(\varvec{q}^+\) satisfies \(S \varvec{q}^+= \varvec{\Pi }\) and is the unique solution to the equation system. Thus, \(\varvec{q}^+\) must also have the property of being in \(\textrm{int}(\Delta ^K)\) and \(\varvec{q}^+ = \varvec{q}^*\). \(\square\)
Market completeness is usually a rather strong hypothesis, while the least-square market includes a broader set of markets. Both the market completeness and the weaker least-squares market conditions enable the use of quantum matrix inversion for finding a martingale measure. Even weaker conditions may also suffice for the use of quantum matrix inversion. For instance, markets where some \(\varvec{q} \in {\mathcal {Q}}\) is \(\varepsilon\)-close to \(S^+\varvec{\Pi }\) may also be good candidates. Another case could arise in the situation where there is a vector \(\varvec{v}\) in the null space of S such that \((\varvec{q}^+ + \varvec{v}) \in \mathcal {Q}\). We leave the exploration of weaker assumptions for future work. In the following theorem, we assume block-encoding access to the matrix S, as per Definition B.2 in the Supplementary Material.
Theorem 5
(Quantum pseudo-inverse pricing in incomplete least-squares markets) Let \((\varvec{\Pi }, S)\) be the price system of a least-squares market with the extended payoff matrix \(S\in \mathbb {R}^{(K+N+1)\times (K+N+1)}\) satisfying \(\Vert {S}\Vert _2 \le 1\) and \(\kappa (S) \ge 2\). Let \(U_{S}\) be a \((\mu (S), 0)\)-block-encoding of matrix S, and assume to have quantum access as Definition B.1 in the Supplementary Material to the extended price vector \(\varvec{\Pi }\in \mathbb {R}^{(K+N+1)}\) and the extended derivative vector \(\varvec{D} \in \mathbb {R}^{(K+N+1)}\). Let \(\gamma \in [0,1]\) and \(\sqrt{\gamma } \le \Vert P_{\mathrm{{col}}}(S)\vert \varvec{\Pi }\rangle \Vert _2\), where \(P_{\mathrm{{col}}}(S)\) is the projector into the column space of S. For \(\varepsilon > 0\) and \(\varvec{q}^+ := S^+ \varvec{\Pi }\), there is a quantum algorithm that estimates \(\Pi _{D,\varvec{q}^+}:= \varvec{D}^T \varvec{q}^+\) with absolute error \(\Vert {\varvec{\Pi }}\Vert _2\Vert {\varvec{D}}\Vert _2 \varepsilon\) and high probability using \({\widetilde{O}}\left( \frac{\kappa (S)\mu (S)}{\varepsilon \sqrt{\gamma }} \right)\) queries to the oracles.
We leave the proof in the Supplementary Material. Interestingly, when the market is complete, the factor \(\sqrt{\gamma }\) is 1, so we can think of this parameter as a quantifier of market incompleteness, which is reflected in the run time of our algorithm (and can be estimated with amplitude estimation). In addition, we can recover an classical approximation of the risk-neutral measure \(\varvec{q}^+\). Obtaining an estimate of \(\varvec{q}^+\) allows us to price derivatives classically. We can use tomography (Theorem B.6 in the Supplementary Material) which in general incurs a cost of K, or we can use weaker models of tomography such as \(\ell _\infty\) tomography or classical shadows to extract useful information.